Overview
On 2nd of October 2019, the ECB first published €STR, an overnight interest rate which effectively replaces EONIA within the EU benchmark reform framework. For the transition period, until 3rd January 2022, EONIA is still published as a 8.5 basis points spread above €STR. The ECB working group on euro risk-free rates made the recommendation to switch interest paid on collateral from EONIA to €STR. While different approaches for the transition were considered, the preferred one was a so called "big bang" introduction: moving completely away from EONIA to €STR flat while compensating for PnL implications due to the 8.5 basis points spread between the two reference rates. Central counterparties (CCPs) followed the recommendation and will move to €STR discounting on or around 22nd of June 2020. On that date, CCPs will conduct a one off compensation mechanism to neutralize the PnL effects on members portfolios.
For swaption holders the above approach can be rather problematic, as many swaptions reference to cleared underlyings (either a physically cleared swap or a collateralized cash price type of settlement). With that link to a cleared swap, the valuation of a swaption depends on the CCPs methodology of discounting and is therefore affected by the "big bang". Now the problem is that the compensation mechanism of the CCP is not "eligible" for all those swaptions that haven’t expired before the "big bang" date, as they aren’t in the trade population of the CCP. Compensation can therefore only be addressed in the bilateral relationship between the trading partners. Unfortunately, ISDA — the biggest and most important institution providing legal frameworks for derivative contracts — has no provisions for a discount rate switch in its master agreements. With that missing piece in the documentation, the legal enforceability of a compensation payment is potentially weak. At the moment there seems to be no clear consensus within the industry, whether there should be a compensation for the value effects on swaptions or not. Without that, we are probably on course for huge value transfers on "big bang" day (below we will see that the market is actually "betting" on that outcome).
Before we dive into all the details of the subject, I want to invite you to get in contact to share your views, as the topic is still very "fluid" and interesting to discuss.
How can we derive from the market that "no compensation" is probably the most likely scenario?
There are quotes in the broker market that give us a hint on how the market is pricing that scenario:
1y30y A+500 receiver over 1y30y A+500 payer, CCP LCH, with 100% 1y fwd
30y LCH swap A+500 (all same strike) 60/250
In the above case somebody is willing to buy / sell an 5% in the money receiver swaption, while selling / buying a 5% out of the money payer swaption. The buyer is willing to pay 60c and the seller quotes 250c. To offset the delta from the construct, a cleared swap with the same strike is traded (further note that the two swaptions also have offsetting vega risk). With zero market risk, this instrument should trade at a zero premium. But if you now take into consideration that the cleared swap will be part of the upcoming compensation process, because it is cleared now, and the swaptions will potentially not, because they expire after the "big bang", a positive premium could be warranted. Let us now analyse how likely a "no compensation" is:
The structure has a discount delta of 25.5c. Multiplied by 8.5 we get
217. Those 217c would approximately be the fair mid in case no
compensation is for sure. If we take the mid from the above quote
(155c), we arrive at 71% probability of a "no compensation" scenario.
Another possible source of footprints towards "no compensation" can be cash IRR vs. CCP settled swaptions. The reason is that cash IRR swaptions have a payoff function that is only linked to the observed swap rate at expiry. This swap rate is almost not affected from the switch by €STR. If you now sell a cash IRR swaption straddle and buy a CCP straddle against it, you will (almost for sure) end up with an in the money swap on the CCP leg profiting from the switch to €STR.
Let’s look at the data for some hints if the above has occurred (physical over cash premiums):
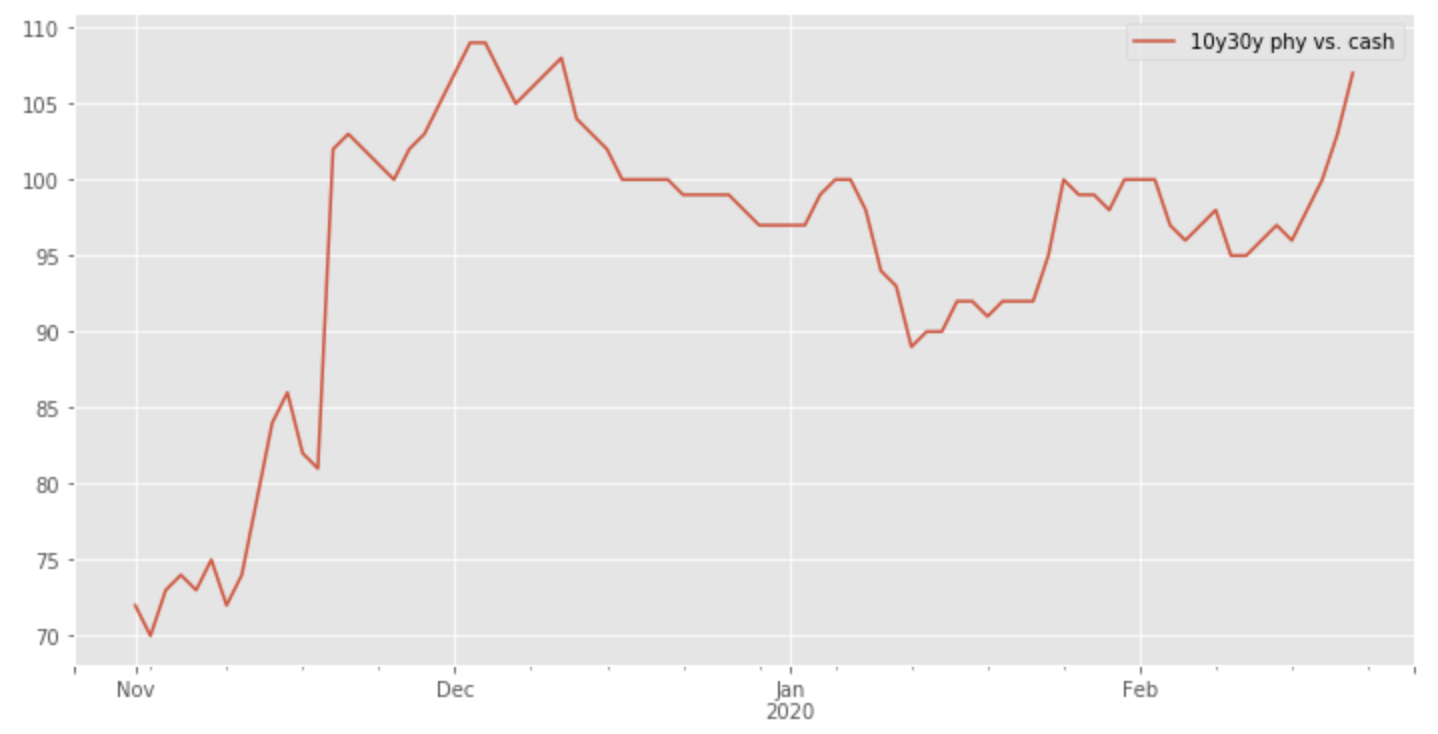
We can see a steep increase in November 2019 which fits our guess of richening physical / cash CCP vs. cash IRR straddles. But we should take this outcome with a pinch of salt as cash IRR straddles are in essence complex CMS products. Also this market is quite illiquid and one-sided. But still, it is another hint at a market pricing in the direction of a "no compensation" scenario.
In summary there is clear evidence that the market is pricing in a high probability for making the transfer to €STR without compensating the discounting difference.
What discount rate do we actually trade when we execute a swaption?
Short answer: it depends. Lets focus first on the dealer market were most of the risk transfer is taking place and from which prices to the buy-side are typically derived. Preferred dealer hedge instrument are swaption straddles. If you have traded a 10y10y swaption straddle at the end of 2018, you would probably have executed it as cash settled instrument based on the CCP methodology and you would have reasonably assumed it is discounted with EONIA till the very end (or at least something that mimics the EONIA discounting value). With the announcement of the "big bang" that has changed, and given you expect no compensation, all straddles that expire post "big bang" are de facto €STR discounted (more precisely the window until expiry will most likely still be EONIA depending on the cash CSA, but from then it is €STR).
With everything that hasn’t a direct CCP link (e. g. swaptions that settle into a bilateral swap, embedded swaptions like callables, cash IRR swaptions) the story is different: Although you might change the cash CSA to €STR in the future, you are completely OK to value those trades with EONIA because you (or your counterparty) will only accept the switch if a compensation payment is paid in return.
If swaptions are completely uncollateralized, your discount rate might involve your own funding spread. As a switch to €STR itself shouldn’t change the absolute rate at which an institutions is borrowing, that discount rate will most likely stay the same.
Brokers started publishing €STR discounted vols along with EONIA discounted vols: Do we need both? Is there a new basis?
Probably finding yet another basis to trade on is one of the most innovative sectors of the financial industry since the financial crisis. But before we start trading that new basis, let’s take a look at the vol surface based on the "old" EONIA annuities:
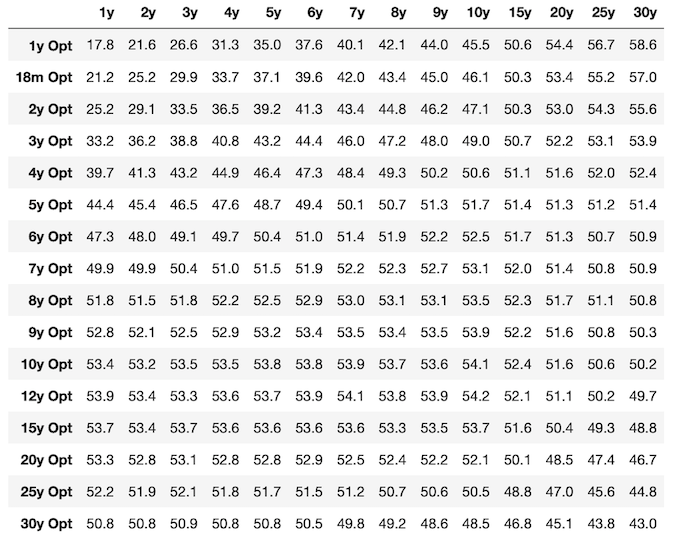
Now, what is the difference when we look at the vols based on €STR annuities? It turns out that those are lower than the ones above. Let’s see by how much:

OK we have a difference, but can it really be the case that 10y10y swaptions have a different volatility depending on the used discount rate?
Depending on the concept of volatility you have in mind, that might sound counter-intuitive. But let’s look at Black’s world and how the straddle (forward) premium is defined (with t the option expiry, T the underlying maturity, r the interest rate, and sigma the Black normal vol):
The above is the straddle price in a Black normal world. The left part is the annuity and in square brackets we can see sigma or the annual bp vol. From the formula it becomes clear that we can only hit the same price (and there is only one price for each straddle) under a different annuity when we simultaneously change the sigma. Now it should become clear that there are not two vols that can co-exist in parallel in our framework. It’s rather that you have to make up your mind which is the appropriate annuity (the market says €STR!), back out the associated vol, and throw away the other vol because ultimately there is only one vol to every straddle.
Nonetheless, it can be useful to think in terms of two vols when you look at certain pricings:
Say you are pricing a callable and your system still is on an EONIA curve framework. Your machine should hit the straddle price as your reference for pricing pretty well (a good thing!). But now comes the problematic part: because of the EONIA annuity it backs out a too high vol, which it uses in the subsequent callable pricing. Here the concept of a second vol comes in quite handy because the difference is a good proxy for the error you are making in the pricing. Say the vol is half a bp lower and you have 100k vega on your callable: that means you are marking the callable 50k too high (because of not being exactly at the money, the effect is a bit overstated)
Which prices do we hit with our old EONIA based valuation framework?
At a first glance and from the above it might be tempting to say: OK, I got the wrong framework for €STR swaptions, so I won’t hit the prices in that area. But clearly, on a second thought, we plug in the wrong inputs (EONIA vols + EONIA annuity) and therefore come up with the right answer: We hit the premiums traded on swaptions in the dealer market. So unfortunately it is (mainly) the swaptions with "real" EONIA underlying that we price inaccurately, as you can see below:
-
✓ ATM Straddles (CCP cash / physically cleared)
-
✓ OTM Payers / Receivers (CCP cash / physically cleared)
-
❏ ITM Payers / Receivers (CCP cash / physically cleared)
-
✓ Cash IRR Swaptions
-
❏ Callables / embedded Options in structured swaps
-
❏ Physically non-cleared Swaptions
How wrong is an EONIA based valuation framework on a portfolio level?
Clearly, finding the exact answer would involve updating the valuation machinery to a proper €STR framework. But at least for a proxy estimate there is no need to do the heavy lifting right away. Unfortunately, we still have to make an assumption, but at least it is a valid one for many portfolios: as a total, the vega from all swaption products, is relatively flat.
In that scenario you can just filter your portfolio on all swaptions with link to a cleared underlying and extract the discount delta from all those trades. Multiplying that number by 8.5 basis points should yield a pretty good PnL estimate.
Just to highlight why a flat position is needed to make that proxy accurate: Say you only have ATM and OTM CCP linked swaptions. Here you are already correct in your valuation and our proxy estimate would only give a zero adjustment if long and short positions cancel out properly.
But now say your total portfolio is flat, but it is not flat with regards to positions in underlyings linked to vs. not linked to a CCP. Here you might correct the value of a ATM straddle you hit, but essentially it the bilateral trade mimicking the vega on the straddle, that you got wrong. So here the proxy is quite good in working out the correct PnL effect.
How would a proper €STR based valuation framework look like?
So now we really want to set everything up in a way that our valuation mechanisms are completely consistent in the new €STR world. As everybody should be familiar with multi-curve frameworks, €STR is only just one more curve added to the already existent curves. But nevertheless, including swaptions imply the need for some further thoughts on how the whole machinery should be set up.
The first important point was already mentioned above: As soon as you start calculating with €STR annuities you will also need — if not implying from premiums — €STR based volatilities.
The second major distinction is hybrid discount curves: Here the rationale is that you might switch from a bilateral underlying to an underlying with CCP link. As those distinct periods may be accompanied with different discounting regimes, there is the need to "split" the discounting into two separate periods.
The illustration below might bring some further clarity to the previously highlighted points:
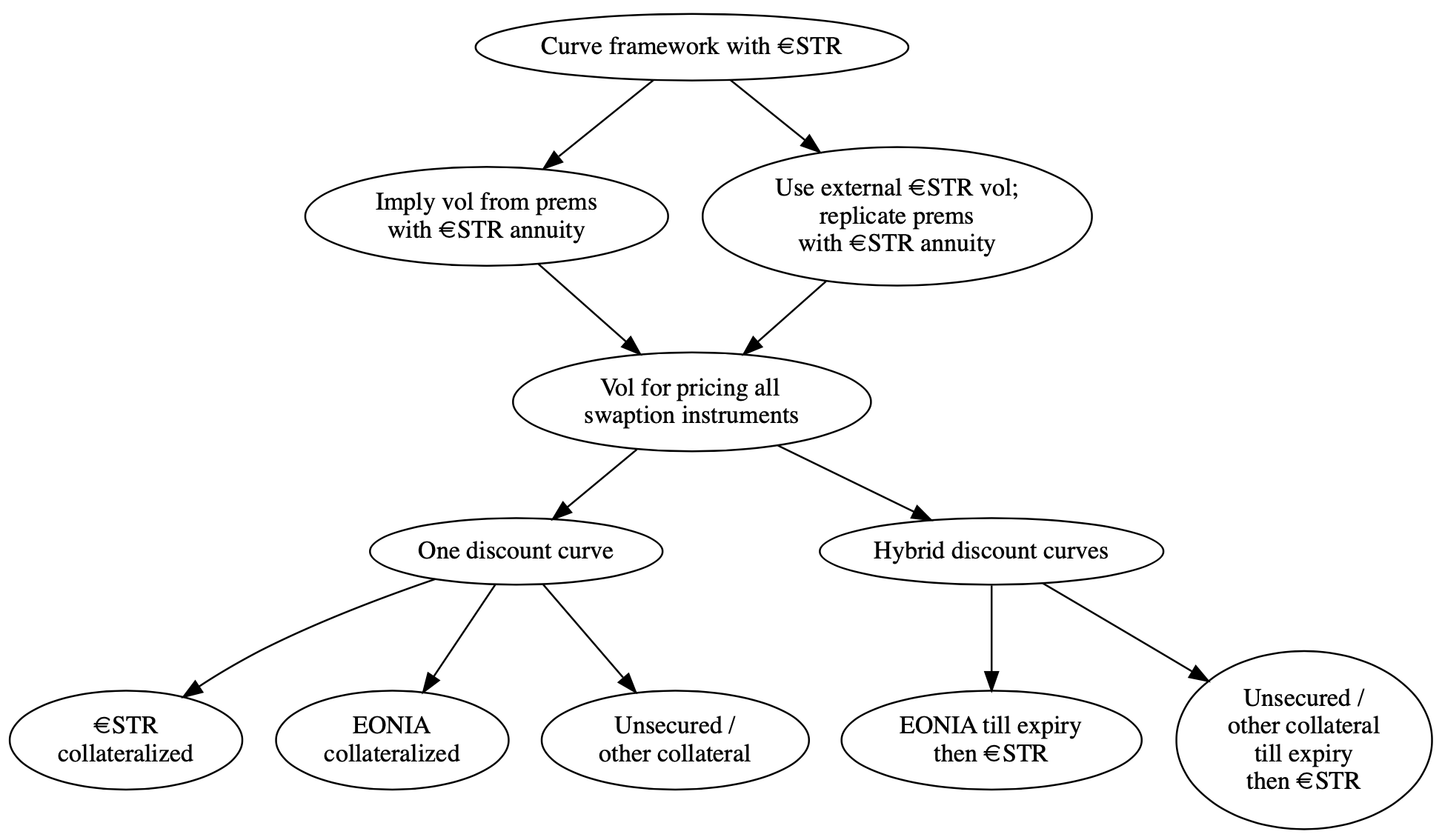
What is the outlook on swaptions with time running out towards "big bang" day?
Above we touched on many aspects related to swaptions approaching "big bang" day. Now we want to come back to the central piece of the matter: which is compensation for the discount effect.
It can be argued that such a switch shouldn’t create winners and losers in market. If we look at the intentional dimension, it probably wasn’t the case that market participants had a value transfer due to discounting in mind when they transacted swaptions in the past. As the instrument was presumably designed for purely reflecting value with regards to an intrinsic and a time value, there could be a will within the industry to preserve that sole function — not at least to show that it can be a reliable hedge instrument in the future.
So there might be a will to find consensus around the
intentional dimension. If that can be achieved in the still going on
initiatives, some agreement / protocol / best practise paving the way
towards compensation might be coming out. But still, even if such an
outcome can be found, it has to be respected by the whole industry to
be effective, as it will probably lack true enforceability.